The Bell state

Bell states are maximally entangled quantum states of two qubits, demonstrating the profound non-classical correlations possible in quantum mechanics.

Quantum computing represents a profound shift in our approach to information processing, leveraging the principles of quantum mechanics to manipulate and process data in ways that classical computers cannot. At the heart of this revolutionary technology are the concepts of superposition and entanglement, which allow quantum computers to perform complex calculations at unprecedented speeds.

Superposition is a fundamental principle in quantum mechanics where a quantum system can exist in multiple states at once. This is unlike classical bits, which are restricted to being either 0 or 1; quantum bits, or qubits, can exist as 0, 1, or any quantum superposition of these states. This property is mathematically represented by:

\(|\psi\rangle = \alpha|0\rangle + \beta|1\rangle \)

where |ψ⟩ is the state of the qubit, and α and β are complex numbers that describe the probability amplitudes of the qubit being in the |0⟩ and |1⟩ states, respectively. The power of superposition lies in the exponential growth of computational space with each added qubit, allowing a quantum computer with n qubits to be in a superposition of up to 2^n different states simultaneously.

Entanglement is another quintessential quantum phenomenon where qubits become interconnected such that the state of one (no matter how far apart) is dependent on the state of another. This can lead to correlations between qubits that are non-intuitive and do not exist in the classical world. For instance, in the Bell state, one of the simplest forms of entangled states, the state of two qubits is described by:

\(|\Phi^+\rangle = \frac{1}{\sqrt{2}} (|00\rangle + |11\rangle) \)

This equation implies that measuring one of the qubits immediately affects the state of its partner, regardless of the distance between them. This property is leveraged in quantum algorithms to perform tasks like quantum teleportation and superdense coding, which can transmit information with efficiencies and security guarantees unachievable by classical systems.

In quantum computing, these principles are utilised through quantum gates, which are the basic operational units that manipulate qubits. Unlike classical logical gates, quantum gates are reversible and can be described as unitary operations. A fundamental quantum gate is the Hadamard gate, which puts a single qubit into a superposition state. It is represented by:

\(H = \frac{1}{\sqrt{2}} \begin{pmatrix} 1 & 1 \\ 1 & -1 \end{pmatrix} \)

When applied to the zero state |0⟩, the Hadamard gate transforms it into a state where the probabilities of measuring a 0 or a 1 are equally likely, as shown:

\(H|0\rangle = \frac{|0\rangle + |1\rangle}{\sqrt{2}} \)

Another pivotal element in quantum computing is the concept of quantum circuits, which are sequences of quantum gates designed to perform specific computational tasks. These circuits exploit the properties of superposition and entanglement to perform parallel computations on all possible inputs simultaneously, thereby potentially solving problems intractable for classical computers. Quantum circuits are often designed to exploit interference effects where probability amplitudes cancel out or reinforce each other, guiding the system toward correct answers while eliminating incorrect ones.

The application of quantum mechanics in computing introduces significant theoretical and practical advancements. Notably, algorithms such as Shor’s algorithm for integer factorisation and Grover’s algorithm for database searching demonstrate that quantum computers can outperform classical computers for specific tasks. Shor's algorithm, for instance, could theoretically break much of the encryption that secures digital communications on the internet by allowing for efficient factorisation of large numbers, a task that is very time-consuming for classical computers:

\(N = pq \)

where N is a large number, and p and q are its prime factors. Shor's algorithm reduces the problem of finding p and q to polynomial time, which is a significant speed-up over the best-known classical algorithms that operate in sub-exponential time.

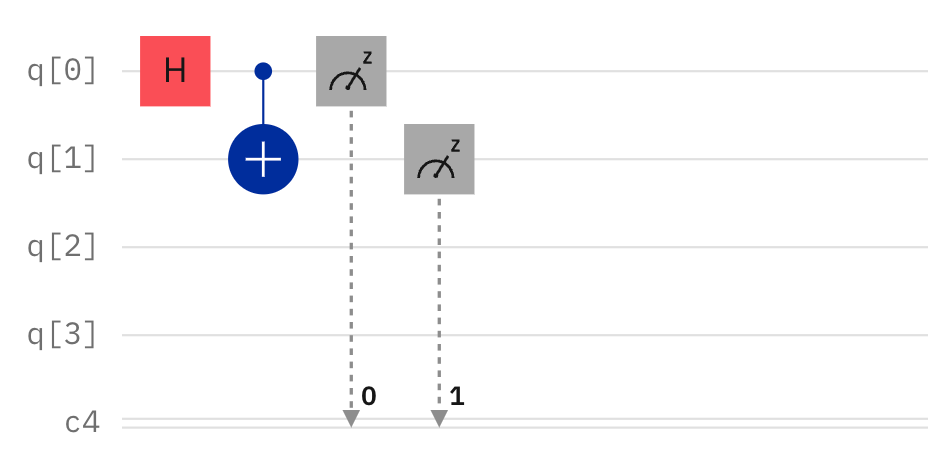
Bell State Circuit

The image above shows a typical a quantum circuit diagram. It includes at least one Hadamard gate (denoted by the 'H' in the red box), which is used to create a superposition of states. The blue plus symbol represents a controlled-NOT (CNOT) gate, which entangles two qubits. Together, a Hadamard followed by a CNOT gate can create a Bell state, a maximally entangled state of two qubits.

Here is the IBM Qiskit code for the circuit:

from qiskit import QuantumRegister, ClassicalRegister, QuantumCircuit
from numpy import pi

qreg_q = QuantumRegister(4, 'q')
creg_c = ClassicalRegister(4, 'c')
circuit = QuantumCircuit(qreg_q, creg_c)

circuit.h(qreg_q[0])
circuit.cx(qreg_q[0], qreg_q[1])
circuit.measure(qreg_q[0], creg_c[0])
circuit.measure(qreg_q[1], creg_c[1])

1. The first qubit (q[0]) is initialised in the state |0⟩ and then passed through a Hadamard gate circuit.h(qreg_q[0]). This places q[0] into a superposition state:

\(H|0\rangle = \frac{|0\rangle + |1\rangle}{\sqrt{2}} \)

2. The second qubit (q[1]) remains in the state |0⟩ until it interacts with the first qubit via a CNOT gate circuit.cx(qreg_q[0], qreg_q[1]). The CNOT gate flips the second qubit if the first qubit is in the state |1⟩. When the first qubit is in a superposition, this results in entanglement between the two qubits, generating one of the Bell states:

\(\text{CNOT}(H|0\rangle \otimes |0\rangle) = \frac{|00\rangle + |11\rangle}{\sqrt{2}} \)

The specific Bell state generated depends on the initial states of the qubits and the structure of the circuit. The circuit could be more complex if it involves more qubits or additional operations. The measurement outcomes suggest that the entanglement indeed causes correlations between the states of qubits such that they are not independent, but the specific details would require a complete view of the circuit.

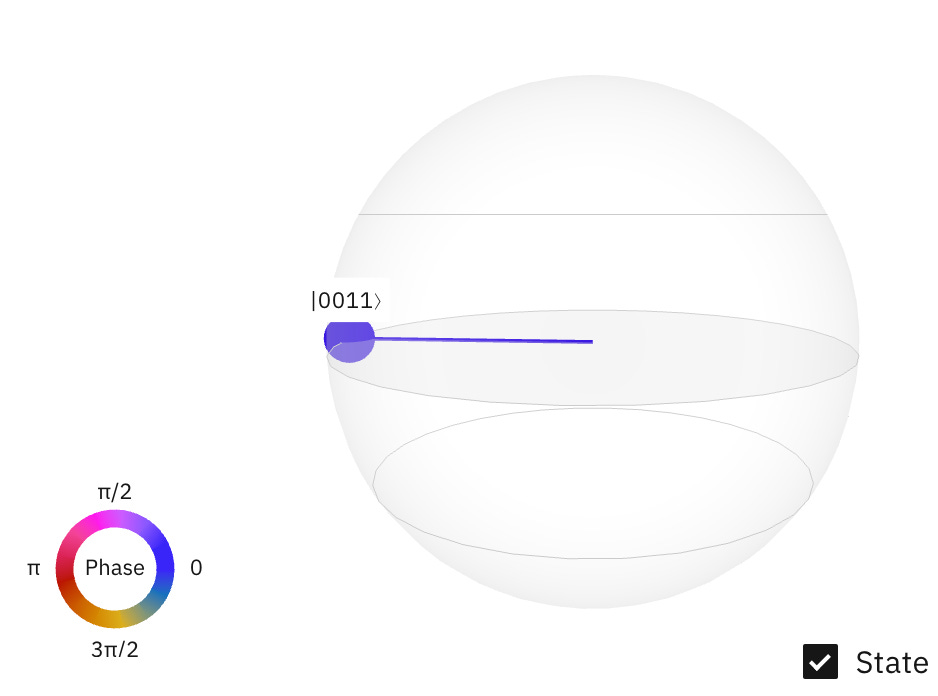
The image above is a representation of a qubit's state on the Bloch sphere, which is a graphical depiction of the state of a qubit in three-dimensional space. The Bloch sphere makes it possible to visualise the superposition of states |0⟩ and |1⟩, as well as the phase differences between them. The point labeled |0011⟩ on the sphere indicates the final state of a qubit system after some transformation has been applied. The specific location of the point on the Bloch sphere suggests that the state has both a real and an imaginary component, corresponding to a superposition of the |0⟩ and |1⟩ states with certain phase relationships.

The last image shows a histogram of measurement outcomes from the quantum circuit which was executed numerous times (often referred to as shots). The x-axis lists possible computational basis states for a multi-qubit system, and the y-axis shows the probability of each state being measured. The bars at |0000⟩ and |0011⟩ indicate that these two states were measured with high probability, suggesting that the quantum circuit is generating a superposition and entanglement of these states.

As quantum technologies continue to evolve, they hold the potential not only for solving specific computational tasks but also for fundamentally altering our approach to science and technology. The development of quantum computers could lead to breakthroughs in materials science, cryptography, and complex system simulation, providing us with insights into phenomena that are currently poorly understood.

While the field of quantum computing is still in its infancy, the theoretical and experimental advancements suggest a future where quantum computers could perform tasks beyond the reach of even the most powerful classical supercomputers. As researchers continue to overcome technical challenges such as error rates and qubit coherence times, the next decades may well usher in an era of quantum supremacy where quantum computers routinely perform calculations that are impossible on classical platforms.